Quelques curiosités topologiques… sur le tore

17 avril 2021
C.Q.F.D.
No comments
Catégories : Sciences

Aujourd’hui, le tore. 

Appelez ça comme vous voulez : une bouée, un donut, une tasse… Oui une tasse, c’est ça la topologie : tout est déformable.  

Mais attention, seulement dans une certaine mesure : on ne coupe pas, on ne perce pas de trous, on joue seulement à la pâte à modeler (et voilà, j’ai perdu toute crédibilité). 

La topologie, c’est avant tout une forte envie d’abstraction et une imagination débordante pour créer de nouveaux mondes. Des objets du quotidiens qui peuvent se révéler sources de nombreuses interrogations, voire de paradoxes dans notre monde à trois dimensions (Ah oui parce que la topologie c’est aussi le voyage entre plusieurs dimensions).  

1 – Des trous, des p’tits trous 

Votre pull, combien a-t-il de trous ? Ou bien votre mug, compagnon de vos nuits de révisions… La notion de “trous” en topologie est un peu différente de celle qu’on peut avoir au premier abord. Pour le pull, disons le col, les deux manches et la taille, soit 4 trous. Dommage, vous y étiez presque ! Maintenant, essayez de faire passer votre main d’une part et d’autre du pull si l’une des manches est nouée, plus les deux, puis le col… Zut, à moins de ressortir par le point d’entrée, vous ne pouvez plus sortir la main de votre pull. On a “bouché” trois entrées et il n’est plus possible de sortir par un autre accès. On dira donc que le pull à 3 trous topologiques. Et pour la tasse ? Là vous auriez peut-être juste en disant que l’anse est l’unique trou, et vous avez raison. Après la même opération que pour notre pull, on retrouve une sphère (après une brève déformation), sphère qui n’a aucun trou (si ce n’est pas le cas, allez vous plaindre qu’on ne vous file pas du matos de qualité !).  

Pour mathématiser un peu tout ça, on peut dire qu’on se ramène à un cercle (pour le pull), sphère et autres hypersphères (à partir de la 4D) au bout d’un certain nombre d’opérations de “bouchage de trous” (Restons dans le champ des maths s’il-vous-plaît).  

Notre ami le tore a donc un unique trou (rappelons qu’il s’agit de la même figure topologique que la tasse). 

  2 – Mario Bros

Dans sa toute première version sortie en 1938 sur borne d’arcade, le plombier américano-italien s’initiait à la topologie.  

Ses déplacements étaient très simples : aller à gauche, à droite, descendre ou monter. La spécificité se trouve lorsqu’il atteint un des bords gauche ou droite ; à ce moment, il passe de l’autre côté, comme si les deux points opposés sur l’écran étaient en fait les mêmes. Avec un peu de recul, on peut facilement imaginer que le plan sur lequel notre ami se déplace est en fait un cylindre, et qu’en allant d’un tuyau à un autre, Mario ne fait que tourner en rond. D’autres jeux comme PacMan ont les mêmes espaces de déplacement.  

Cependant, on n’a pas là un espace torique, mais seulement cylindrique. 

La manipulation topologique – impossible à réaliser dans notre monde non déformable – serait alors de relier également les points Nord aux points Sud, c’est-à-dire relier les deux extrémités (cercles) du cylindre obtenu au départ (Si Mario tombe des briques, il se retrouve en haut et inversement). La figure topologique de ses déplacements serait alors cette fois ci un tore.  

3 – On va un peu plus loin ?

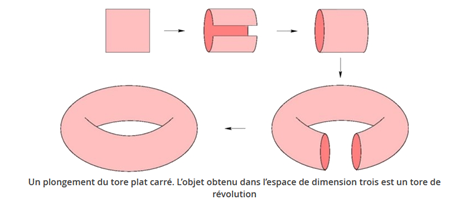
On est content, on a notre tore (de révolution, soyons précis) pour équivalent topologique à notre espace de jeu vidéo en dimension 2 (qui est au passage appelé un tore plat carré). Mais un problème persiste : au cours de nos transformations (passage du cylindre au tore), on a dû fortement déformer la figure, au prix de distances faussées. La question de nombreux mathématiciens est alors toute simple : “Est-il possible de représenter un tore plat carré sans déformer les longueurs ?” Au passage, ce genre de représentation respectant également les distances est appelée plongement isométrique. 

En prémisse à la résolution de cette question, et contrairement à l’intuition qu’on pourrait avoir, les mathématiciens J. Nash et N. Kuiper montrent que non seulement une figure de ce type existe mais en plus qu’il en existe une infinité. Ces figures semblent par contre n’avoir pas les mêmes propriétés « esthétiques » de régularité / symétrie, etc. comme peuvent avoir la sphère ou le tore (cette irrégularité s’exprime par le fait que les courbes mises en jeu n’admettent pas de tangentes). 

Nouveau problème, plus subtil cette fois-ci, comment trouver une surface de ce type qui soit bien “lisse” et « policée », au même titre que le tore ? L’idée est ici de “simplifier” la figure, comme on pourrait le faire pour la tasse (“irrégulière”), en un tore. 

Et c’est là que l’imagination mathématique s’enclenche… 

Avec le développement de nouveaux outils mathématiques (intégration convexe) dans les années 70-80, il devient possible de mieux décrire la mise en problème de Nash et Kuiper. 

Ces “intégrations convexes” permettent d’opérer à un retournement de la sphère (je ne vais pas entrer dans les détails, quelques articles et vidéos sont à retrouver en fin d’article pour les plus curieux d’entre vous – spoiler : c’est très intéressant -). Alors pourquoi ne pas tenter sur notre tore ? 

Quand vous froncez des sourcils ou quand vous plissez des yeux, votre peau se corrugue.  Elle a tendance à se replier sur elle-même. Imaginez que chacune de ces corrugations se corrugent elles-mêmes (non ne partez pas !), et bien c’est ce principe “simple” qui a été utilisé chez notre ami le tore. 

  4 – Quelques corrugations et en route vers les fractales !  

C’est en 2012 qu’une équipe de chercheurs en Mathématiques et Informatique (de Lyon & Grenoble) réussissent à construire une figure topologique respectant le prolongement isométrique du tore plat carré (nom de projet : Hévéa). Grâce aux nouveaux outils mathématiques (d’intégration convexe), les chercheurs imaginent un algorithme qui, comme on pourrait le faire sur notre peau, corrugue le tore initial. Sauf qu’ils ne s’arrêtent pas là et poursuivent la corrugation une deuxième fois sur chacune des corrugations déjà existantes, puis une troisième fois, et ainsi de suite à l’infini. Avec ce processus, les distances restent inchangées d’une corrugation à l’autre. Ça tombe bien, c’est ce qu’on voulait ! 

Cette nouvelle figure, dont la géométrie ressemble (de loin !) à celle du tore initial, pose de nouvelles questions. Comme on a réalisé une infinité de fois ces opérations de corrugations (c’est la dernière fois que j’écris ce mot, promis – d’ailleurs, c’est le principe d’intégration convexe qui s’exprime ici par les corr…), si l’on se balade et que l’on zoome, encore et encore, ne va-t-on pas retrouver le même schéma à l’infini, sans en percevoir le bout ? Cet objet mathématique est à mi-chemin* entre une fractale (objet infiniment fracturé quelle que soit l’échelle à laquelle on l’observe) et une surface lisse ordinaire… Mais ça, c’est une autre histoire. 

* La nuance se trouve dans l’emploi du mot “fracture” dans la définition des fractales. Ici, notre tore 2.0 est constitué d’une infinité de corrugations (oups, je ne tiens pas mes promesses dans l’astérisque), qui sont “lisses” et possèdent des tangentes, contrairement aux fractales.  

Robin

Sources :  

Images :  

Derniers articles :

  • Familles Disparues, Épisode 2: Les Spinosauridés
                Bonjour et bienvenue dans ce second épisode dédié à nos chers animaux disparus, et désolé  du petit délais géologique depuis le dernier article ! Aujourd’hui nous parlerons d’énigmatiques […]
  • La chronique des hobbies
    La petite chronique où nous venons vous présenter nos hobbies ! Bonjour tout le monde ! Bienvenue dans ma chronique ! Venez venez ! Je vais vous présenter mes […]
  • Les bâtiments du campus
    Grignard, Forel, Dubois, Lwoff… vous êtes tous déjà passés devant ces bâtiments, mais vous êtes-vous déjà demandé qui ils honoraient ? J’ai mené l’enquête pour vous, armé de Wikipédia et […]
  • Chasse aux fossiles à la Doua
    Vous y allez tous les jours (ou presque) pour suivre vos cours, réviser à la BU, squatter votre local associatif préféré et bien d’autres choses encore, mais connaissez-vous vraiment […]
  • Les échappées littéraires : La divine vérité (Nouvelle)
    Bonne année à toutes et à tous ! Inaugurons ensemble 2022 avec une nouvelle échappée littéraire en partenariat avec l‘atelier d’écriture de Nouvelle de la Mission Culture. Aujourd’hui : […]
  • Vignette de l'article
    Du jeu vidéo devant ma cheminée
    Et Mariah Carey dedans
  • Le redoublement, ce n’est pas si mal que cela !
    Une année non validée, cela est une des craintes de beaucoup d’étudiants. Lorsque c’est le cas, la question du redoublement se pose alors. En vaut-il l’effort ?
  • Science à voir Épisode 11 : Podcasts
    Aujourd’hui : changement de longueur d’onde   Plongez dans le monde des productions radiophoniques, de ces créateurs et créatrices dont on ne connaît que la douce voix, des jingles entêtants, des […]
  • Vignette "Remake, reboot, remaster et réchauffé"
    Remake, reboot, remaster et réchauffé
    On ne change pas une équipe qui gagne. 
  • image illustrative des chroniques naturalistes, avec simbakubwa kutokaafrika
    À la découverte de… Simbakubwa kutokaafrika
    Doté d’une mâchoire deux fois plus grande qu’un crâne de Lion d’Afrique, cet impressionnant Mammifère terrestre n’est ni une hyène, pas plus qu’un lion. Qui est-il ? Pour le savoir, nous vous emmenons à la découverte de Simbakubwa kutokaafrika !